AMMs 101
Aug 21, 2023
How do DEX Automated Market Makers work?
A market maker (MM) is an entity that creates the trading environment for a particular asset by offering the prices at which traders engage with the asset and managing the liquidity.
Decentralised exchanges (DEX) have automated market makers – they use maths and algorithms to balance liquidity in the asset pools via token price - Automated Market Makers (AMMs). There are a few different types of algorithms such as the Constant Product (Uniswap), Constant Mean (Balancer), and Stableswap Invariant (Curve) make up most of the market.
Now, that being said, the AMMs we explore in this article are older and simpler. The reason for this is that we will release an AMMs 201 article in the future exploring the newer innovations, but understanding how these older models work is important as a foundation.
Let’s dive into each of these, but first, a quick note: we have attached an Excel file (at the end) with the calculators for each market maker allowing you to work out slippage and pool allocation after trades. Enjoy!
P.S. trading fees have been ignored for these calculations.
How do Constant Product Market Makers (CPMM) work?
x * y = k
x is the number of assets X
y is the number of assets Y
k is the constant – the multiple of the two
This was one of the first automated market makers to be implemented by Uniswap.
Once the pool is created and initial liquidity is deposited, whatever k the x * y make, that’s the k that the pool will try to keep if there is a trade that affects one of the assets. The key is that the value of the tokens are in a 50/50 ratio, not the amount of tokens. The value would be in terms of dollar (or other) value of the total amount of each token.
When the supply of token X increases, the token supply of Y must decrease, and vice-versa, to maintain the constant product K. When plotted, the result is a hyperbola where liquidity is always available but at increasingly higher prices, which approach infinity at both ends.
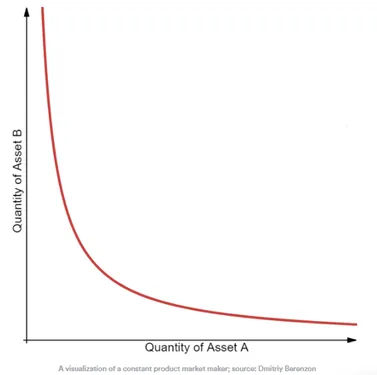
Here, future LPs have to provide tokens in the 50/50 ratio to ensure the price is not impacted when liquidity is provided. This means that if you want to add liquidity, you need to add both assets into the pool, otherwise the pool will misinterpret that as a trade and will therefore change the price of the second asset to ensure the constant is the same.
Price and slippage calculation has been implemented in Excel.
How does the Constant Mean Market Maker (CMMM) work?
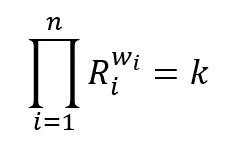
The Constant Mean MM was built on the theory of the Constant Product MM but allows for more than two assets as well as unequal weights. In the formula Ri is the amount of each asset, the wi are the weights, and n is the number of assets.
Balancer, a protocol that has implemented the Constant Mean MM, also added the function that LPs can provide liquidity as single assets. It must be noted that this does affect the relative price of the tokens in the pool, as weights remain unchanged.
The following formula can be used to calculate prices and slippage (these can be derived in needed).
Price of token x in terms of token y:
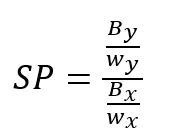
If a trader puts in deltay token y, they will receive deltax token x where:
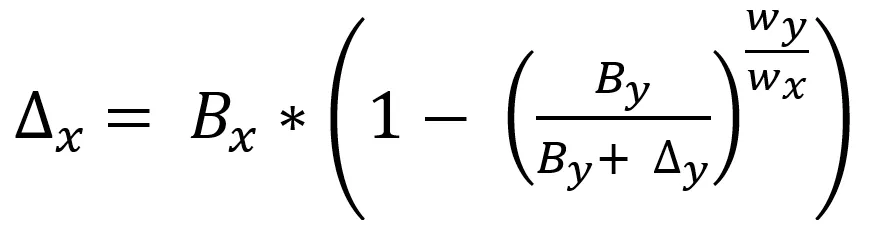
This formula holds regardless of the amount of tokens (n) in the pool.
How does the StableSwap Invariant work?
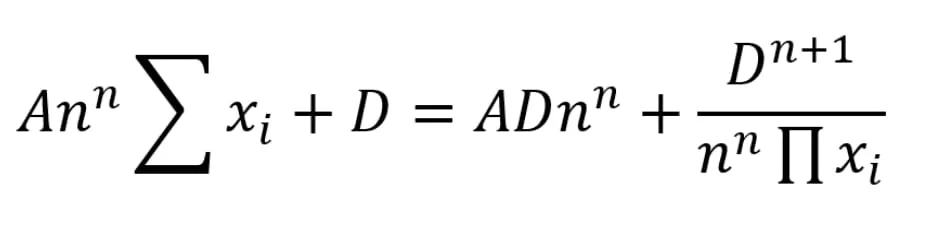
This MM Was implemented and tested by Curve Finance. It is essentially a combination of the Constant Product and Constant Sum MMs. The StableSwap Invariant was designed to be used for assets that are relatively stable to one another in price - it is designed such that the spot price of one asset in terms of other is close to 1 for as long as possible.
The A parameter is used to define the balance between the Constant Product and Constant Sum MMs, noting that when A = 0, the StableSwap Invariant is the same as the Constant Product MM. A can be thought of as the amount of leverage employed by the protocol when the coins are in perfect balance.
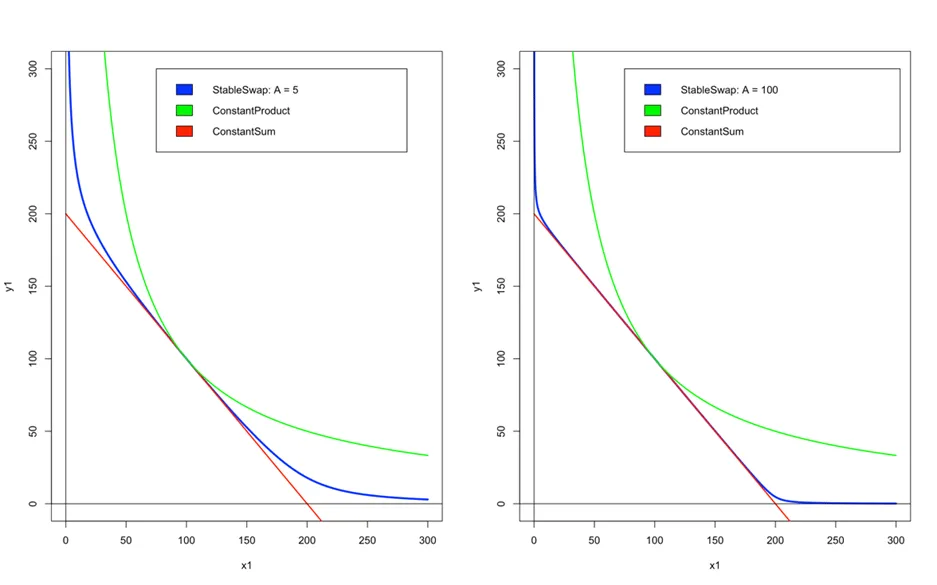
From the figure above, we can see that when A is small (=5) the StableSwap MM acts more like the CPMM, with price stability being provided over a smaller range of x and y values. Whereas when A is larger (=100), the SSMM acts like a CSMM over a larger range of x and y values.
It should be noted, however, that when A is large, the slippage incurred when the assets fall far out of balance is larger than when the assets fall far out of balance when A is small. This can be seen by the gradient of the StableSwap curve at the points where it deviates from the Constant Sum curve.
The D parameter is solved for once A has been specified and liquidity has been provided and is kept constant thereafter. This needs to be solved for numerically whenever there are more than two tokens in a pool, however, a closed form solution can be found when there are only two assets (see Excel).
In excel the slippage on a Constant Product pool can be compared with the slippage on an ‘equivalent’ StableSwap pool. With inputs (X=100, Y=100, A = 85) we see that swapping in 10 of token X in the Constant product pool results in a slippage of 10% but for the stable swap pool the slippage is only 0.059%.
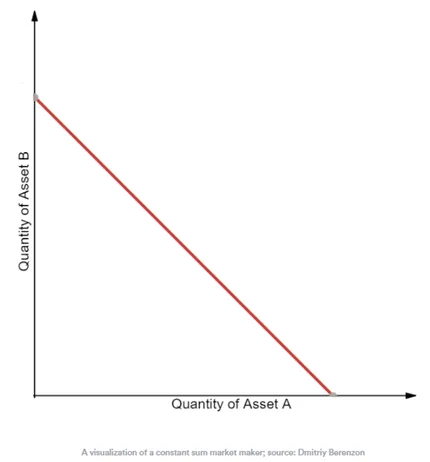
How do Constant Sum Market Makers (CSMM) work?
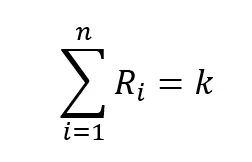
This MM is rarely used. It has the property that the quantity of one token in terms of the other will always be at a ratio of 1:1, regardless of the price of each. This means that there is no slippage, but it does not provide infinite liquidity like the CPMM – an arbitrageur can drain the reserve to zero if the price of either token on an outside exchange changes.
How it would work:
Initial liquidity: 100X and 100Y
K = 100X + 100Y = 200
Buy 50X
200 = 150X + _Y
Therefore, pay 50Y for 50X
Price paid = 50/50 = 1
What AMM is best?
The idea here isn’t that one AMM is better than the other, but that different AMMs have different liquidity provision mechanisms and therefore you need to understand how each of them works to be able to provide the correct liquidity for the DEX you’re launching on.
Uniswap’s pioneering technology allows users to create a liquidity pool with any pair of ERC-20 tokens with a 50/50 ratio, and has become the most enduring AMM model on Ethereum.
Balancer stretches the limits of Uniswap by allowing users to create dynamic liquidity pools of up to eight different assets in any ratio, thus expanding AMMs’ flexibility.
Curve specializes in creating liquidity pools of similar assets such as stablecoins, and as a result, offers some of the lowest rates and most efficient trades in the industry while solving the problem of limited liquidity.
https://www.gemini.com/cryptopedia/amm-what-are-automated-market-makers#section-automated-market-maker-variations
Should I launch on a DEX or a CEX?
DEXs offer an inherent trustlessness due to market making happening algorithmically.
Centralised exchanges utilise independent entities called Market Makers to make the market for the traders via order books, instead of an algorithmic automatic market maker that DEXs utilise. This means that if you or the CEX utilises a bad market maker, it will be more problematic than simply launching on a DEX.
We spent $40k for a listing in a CEX that was top 15 [Coin Market Cap] at the time + added about $30k (tokens and USDT) for "market making" + a bunch of tokens for "promotions" and "competitions". They promised marketing and what not.
In reality:
1. We got NO real users to join our project.
2. Their market making team drained the account in about 2 months, so the volume dropped significantly right after.
3. Not only did our token not grow, they actually dumped the price.
4. We ended up getting delisted after a few months for lack of volume (basically we didn't want to keep sending money to do market making).
DEXs make a lot more sense in my opinion if the project knows how to get liquidity. - Founder of Optimus Ventures
That being said, it is equally possible to completely mis-utilise the DEX AMMs, for instance by not depositing the correct amount of liquidity or simply not enough liquidity, thereby causing incredible slippage and volatility that wont happen with a CEX.
A project just needs to understand what will happen with their token, as most problems occur from a lack of information.




